Berechnen eines Normalenvektors einer Ebene mit einer Koordinatenform der Ebene:
Wir wollen den Normalenvektor einer Ebene aus einer Ebenengleichung in Koordinatenform bestimmen. Dazu beginnen wir mit einer Gleichung der Ebene, die den Normalenvektor
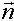 enthält: Die Normalenform der Ebene
enthält: Die Normalenform der Ebene 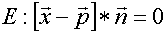 .
.Dabei ist
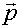 der Stützvektor,
der Stützvektor, 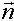 der Normalenvektor und
der Normalenvektor und 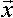 der Ortsvektor irgend eines Punktes der Ebene E.
der Ortsvektor irgend eines Punktes der Ebene E.Wir schreiben die Normalenform ausführlicher und formen sie geeignet um:
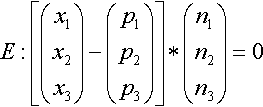
Bei der Skalarmultiplikation gilt wie bei der normalen Multiplikation das Distributivgesetz:
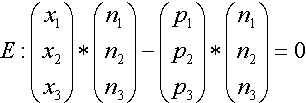
Durch Anwenden der Skalarmultiplikation erhalten wir:
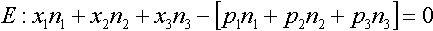
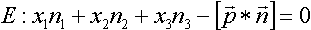
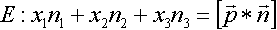
Mit
 (dabei ist d als Skalarprodukt zweier Vektoren eine reelle Zahl) folgt
(dabei ist d als Skalarprodukt zweier Vektoren eine reelle Zahl) folgt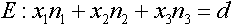
Durch Anwenden des Kommutativgesetzes erhalten wir
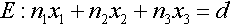 .
.Wir erhalten also durch einfache Äquivalenzumformungen aus der Normalenform der Ebenengleichung eine Ebenengleichung in Koordinatenform!
Und erstaunlicherweise sind die Koeffizienten der Normalenform genau die Koordinaten des Normalenvektors!
? Beispiel ?
| Links zur besseren Navigation: | |||
| Home | Winkel oder Abstand | Skalarprodukt | Betrag |
| Normalenform | Normalenvektor | Definition Abstand | Definition Winkel |