Betrag eines Vektors
(Länge eines Vektors):
Zunächst am Beispiel:
Wir betrachten einen Quader, dessen Kanten auf den Achsen des Koordinatensystems liegen:
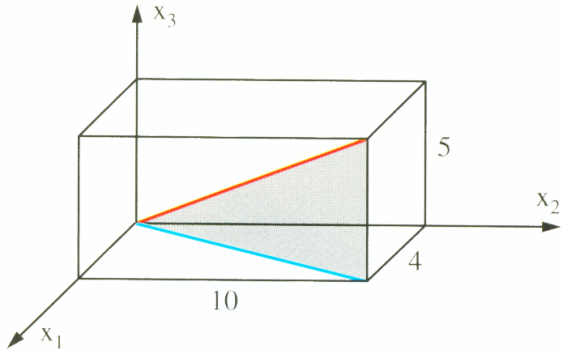
Die Länge der blauen Diagoale dblau (also die Diagonale der Grundfläche) berechnen wir mit dem Satz des Pythagoras:
dblau=
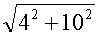
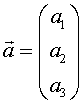 des Punktes A(a1 / a2 / a3).
des Punktes A(a1 / a2 / a3).Im Beispiel von Oben zeigt dieser Ortsvektor vom Ursprung zum Punkt A(4/10/5), er wird also durch die rote Diagonale repräsentiert.
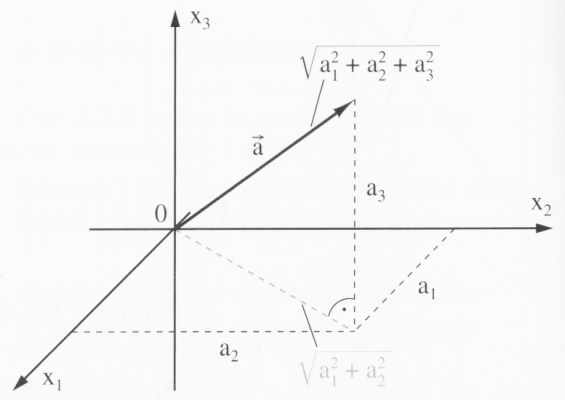
Analog zum Beispiel berechnen wir jetzt nicht die Länge einer Raumdiagonalen, sondern den Betrag eines Vektors.
Offensichtlich ist der Rechenweg derselbe!
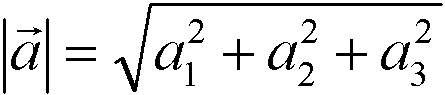
| Links zur besseren Navigation: | |||
| Home | Winkel oder Abstand | Skalarprodukt | Betrag |
| Normalenform | Normalenvektor | Definition Abstand | Definition Winkel |