Normalenform der Ebenengleichung
Wir haben anschaulich schon gesehen, was ein Normalenvektor ist: er steht senkrecht zu einer Ebene, genauer gesagt zu jedem Spannvektor der Ebene.
Diese Tatsache ist ganz praktisch, denn man kann so mit einem Stützpunkt und einem Normalenvektor eine Ebenengleichung angeben.
Im Vergleich zur Parameterform (dort benötigen wir einen Stützpunkt und zwei Spannvektoren)
benötigt man also einen Vektor weniger um eine Ebene eindeutig zu beschreiben.
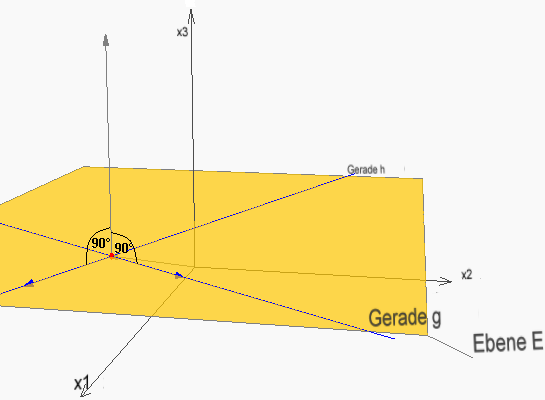
Ist ein Normalenvektor bekannt, kann man die Ebene E direkt angeben.
Definition: Ist P Aufpunkt/Stützpunkt mit Stzützvektor 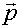 , und , und 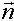 Normalenvektor einer Ebene E, dann heißt Normalenvektor einer Ebene E, dann heißt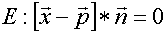 Normalenform der Ebene E. Normalenform der Ebene E.Dabei ist 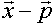 anschaulich der Verbindungsvektor vom Stützpunkt zu einem
beliebigen
Punkt X, der in der Ebene liegt.
anschaulich der Verbindungsvektor vom Stützpunkt zu einem
beliebigen
Punkt X, der in der Ebene liegt. |
Bei uns ist der Normalenvektor aber noch nicht bekannt, wir müssen ihn zuerst berechnen.
Wie viele Normalenvektoren zu einer Ebene gibt es?
| Links zur besseren Navigation: | |||
| Home | Winkel oder Abstand | Skalarprodukt | Betrag |
| Normalenform | Normalenvektor | Definition Abstand | Definition Winkel |