Beispiel der Berechnung des Abstandes einer Ebene und einer zu ihr parallelen Geraden:
Wir betrachten die Ebene
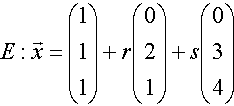 und die zu ihr parallele Gerade
und die zu ihr parallele Gerade 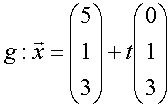 .
.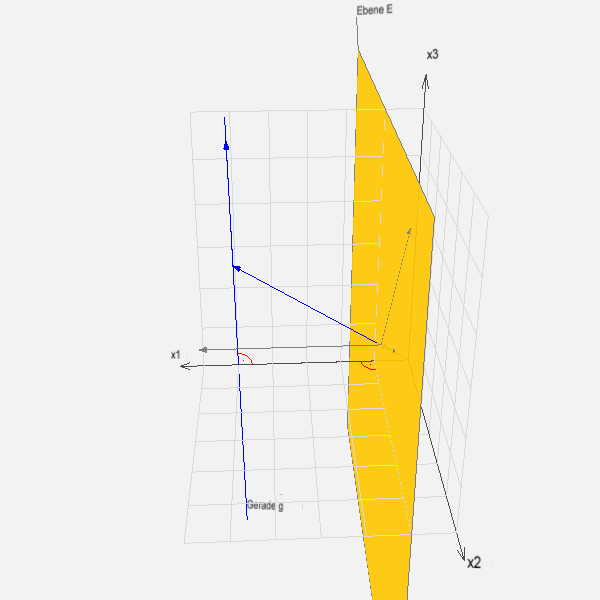
Vektoris3D gibt als Abstand d = 4 an.
Wir berechnen einen Normalenvektor
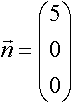 und erhalten mit ihm und einem Punkt der Geraden g (am einfachsten wählt man den Stützpunkt)
und erhalten mit ihm und einem Punkt der Geraden g (am einfachsten wählt man den Stützpunkt)eine Geradengleichung der Lotgeraden h in Parameterform:
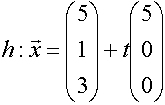 .
.Durch Gleichsetzen der Ebenengleichung mit der Lotgeraden h erhalten wir ein LGS mit genau einer Lösung.
(Das muss so sein, weil die Lotgerade die Ebene schneidet).
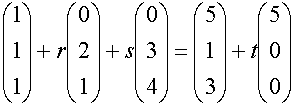
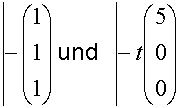
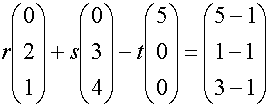
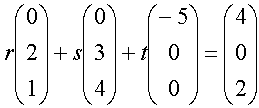
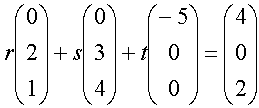 .
.Wir erhalten das LGS
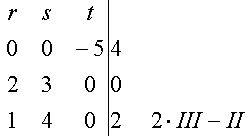 und
und 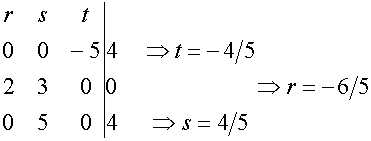
Durch Einsetzten der Parameter t in h ODER r und s in E erhalten wir den Lotfußpunkt
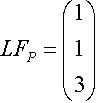 .
.Jetzt berechnen wir den Abstand vom Lotfußpunkt LFP zum Stützpunkt P der Geraden,
weil dieser Abstand als Abstand der Ebene E und der Geraden g definiert ist.
Dazu berechnen wir den Betrag des Verbindungsvektors der beiden Punkte:
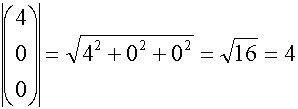 .
.Somit haben wir den von Vektoris3D vorgegebenen Abstand überprüft!
| Links zur besseren Navigation: | |||
| Home | Winkel oder Abstand | Skalarprodukt | Betrag |
| Normalenform | Normalenvektor | Definition Abstand | Definition Winkel |