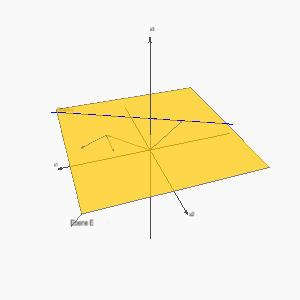
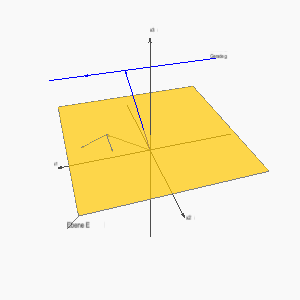
Algebraische Unterscheidung der Lagebeziehungen:
Aus der Anschauung kennen wir diese Fälle:
Algebraische Betrachtung:
In allen Fällen erhalten wir eine Gleichung durch Gleichsetzen der Ebenengleichung und der Geradengleichung.
Beispiel:
Sind 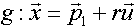 und
und 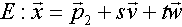 , dann erhalten wir durch Gleichsetzen von g und E:
, dann erhalten wir durch Gleichsetzen von g und E:
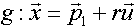 und
und 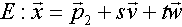 , dann erhalten wir durch Gleichsetzen von g und E:
, dann erhalten wir durch Gleichsetzen von g und E:g = E
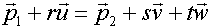
und durch geeignetes Umformen
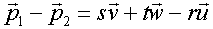
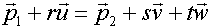
und durch geeignetes Umformen
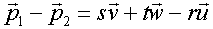
Diese Vektorgleichung können wir als LGS schreiben. Für die Lösung dieses linearen Gleichungssystems gibt es drei Möglichkeiten:
| Das LGS hat genau eine Lösung Die Ebene und die Gerade haben einen gemeinsamen Punkt. Die Gerade schneidet die Ebene Setzt
man die Parameter dieser Lösung entweder in die Ebenengleichung oder in
die Geradengleichung ein, so kann man den Schnittpunkt berechnen. | Das LGS hat unendlich viele Lösungen Ebene und Gerade haben unendlich viele gemeinsame Punkte. Die Gerade liegt in der Ebene | Das LGS hat keine Lösung Die Ebene und die Gerade haben keine gemeinsamen Punkte. Ebene und Gerade sind parallel |
Betrachtet man die Fälle "Die Gerade schneidet die Ebene" und "Gerade und Ebene sind parallel" genauer, so erkennt man Unterschiede im Schnittwinkel und im Abstand der Geraden zur Ebene.
Wie kann man den Schnittwinkel zwischen einer Gerade und einer Ebene berechnen?
Wie kann man den Abstand zwischen einer Ebene und einer zu ihr parallelen Geraden berechnen?